
«En todo triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos«. Pitágoras de Samos
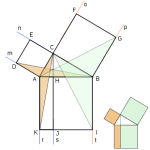
Hay cientos de demostraciones de este teorema ( E. S. Loomis, catalogó 367 pruebas diferentes, otros autores hablan de 1000), más que para cualquier otro teorema matemático. Estas pruebas han sido ideadas por gente de muy diferente condición entre la que se incluye a un mago babilonio, un estudiante de Ohio de 14 años de edad con un nivel intelectual normal, el genio de las matemáticas de 21 años Galois, así como James A. Garfield, que se convirtió en presidente de los Estados Unidos en 1881.
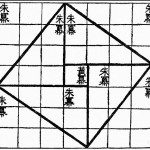
Una tradición muy persistente con base documental en Vitrubio, Plutarco, Diógenes Laercio, Ateneo y Proclo, atribuye el Teorema de Pitágoras al propio Pitágoras. Pero los descubrimientos arqueológicos de los restos de las culturas de Mesopotamia, Egipto, India y China, han revelado que estas civilizaciones conocían aspectos del Teorema de Pitágoras muchos siglos antes que este sabio. Las referencias prehelénicas al Teorema no contienen, sin embargo, pruebas del mismo, mientras que es generalizada la creencia de que fue Pitágoras (o bien alguno de sus discípulos) el primero en proporcionarnos una demostración lógica del Teorema, lo que hará justo que éste haya pasado a la historia con su nombre.
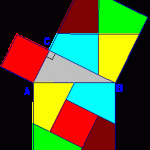
Otra razón importante para la gran cantidad de demostraciones existentes, es que en la Edad Media se exigía una nueva demostración para conseguir el grado de «Magíster matheseos».
Encontramos demostraciones más o menos intuitivas, algebraicas, geométricas y gráficas, (puzzles pitagóricos).
Incluso el arte se ha contagiado del espíritu de éste teorema, que ha inspirado a diversos artistas.

Desde www.cuantaciencia.com nos animaron a construir una de las más sencillas, de manera que de un sólo vistazo y de una manera divertida podemos comprobar que efectivamente, que si un triángulo rectángulo tiene catetos de longitudes a y b , y la medida de la hipotenusa es c, se establece que:
Aquí os presentamos nuestra demostración práctica en un imán de nevera. Sólo tenemos que girarlo para que se rellenen las superficies (volúmenes, pero a efectos visuales los tomamos como superficies) correspondientes a los catetos o a la hipotenusa respectivamente.
Funciona como un reloj de arena, un reloj matemático…. 

 Está disponible en nuestra tienda, si perteneces a un colegio u otro colectivo interesado en adquirir varias unidades ponte en contacto con nosotros para que te hagamos un presupuesto. (Imán Pitágoras en MJ2Artesanos).
Está disponible en nuestra tienda, si perteneces a un colegio u otro colectivo interesado en adquirir varias unidades ponte en contacto con nosotros para que te hagamos un presupuesto. (Imán Pitágoras en MJ2Artesanos).
Referencias:
http://www.librosmaravillosos.com/pitagorasysuteorema/algunasconsideracionespitagoricas.html
http://divulgamat2.ehu.es/divulgamat15/index.php?option=com_content&view=article&id=3326%3Apitras-siglo-vi-ac&catid=37%3Abiograf-de-matemcos-ilustres&directory=67&limitstart=5
http://culturacientifica.com/2013/05/22/cultura-pitagorica-arte/
http://roble.pntic.mec.es/jarran2/cabriweb/1triangulos/teoremapitagoras.htm
http://commons.wikimedia.org/wiki/File:Teorema_de_Pit%C3%A1goras.Euclides.svg
http://culturacientifica.com/2013/05/22/cultura-pitagorica-arte/
